人工智能实践Tensorflow笔记:Tensorflow框架-3
张量tensor:
张量就是多维数组(列表),用“阶”表示张量的维度。
0 阶张量称作 标量scalar
1 阶张量称作 向量vector []
2 阶张量称作 矩阵matrix [[]]
数据类型:
Tensorflow 的数据类型有 tf.float32、tf.int32 等。
计算图(Graph):
搭建神经网络的计算过程,是承载一个或多个计算节点的一张图,只搭建网络,不运算。
会话(Session):
执行计算图中的节点运算。
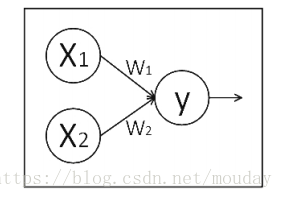
神经网络的参数:
是指神经元线上的权重 w
神经网络中常用的生成随机数/数组的函数
|
函数 |
说明 |
|
tf.random_normal() |
生成正态分布随机数 |
|
tf.truncated_normal() |
生成去掉过大偏离点的正态分布随机数 |
|
tf.random_uniform() |
生成均匀分布随机数 |
|
tf.zeros |
表示生成全 0 数组 |
|
tf.ones |
表示生成全 1 数组 |
|
tf.fill |
表示生成全定值数组 |
|
tf.constant |
表示生成直接给定值的数组 |
神经网络的实现过程:
1、准备数据集,提取特征,作为输入喂给神经网络(Neural Network,NN)
2、搭建 NN 结构,从输入到输出(先搭建计算图,再用会话执行)
( NN 前向传播算法 计算输出)
3、大量特征数据喂给 NN,迭代优化 NN 参数
( NN 反向传播算法 优化参数训练模型)
4、使用训练好的模型预测和分类
训练过程和使用过程
前向传播:
就是搭建模型的计算过程,让模型具有推理能力,可以针对一组输入给出相应的输出。
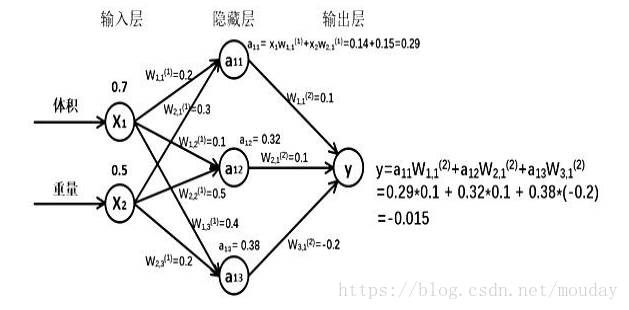
待优化的参数:
W 前节点编号,后节点编号(层数)
神经网络共有几层(或当前是第几层网络)都是指的计算层,输入不是计算层
反向传播:
训练模型参数,在所有参数上用梯度下降,使 NN 模型在训练数据上的损失函数最小。
损失函数(loss):
计算得到的预测值 y 与已知答案 y_的差距。
均方误差 MSE:
求前向传播计算结果与已知答案之差的平方再求平均。
loss_mse = tf.reduce_mean(tf.square(y_ - y))
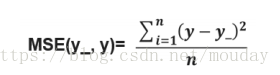
反向传播训练方法:
以减小 loss 值为优化目标,有梯度下降、momentum 优化器、adam 优化器等优化方法。
随机梯度下降算法
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
超参数
train_step=tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss)
自适应学习率的优化算法
train_step=tf.train.AdamOptimizer(learning_rate).minimize(loss)
学习率:决定每次参数更新的幅度。
进阶:反向传播参数更新推导过程
搭建神经网络的八股
准备工作
前向传播
反向传播
循环迭代
linux:
vim ~/.vimrc 写入:
set ts=4 表示使 Tab 键等效为 4 个空格
set nu 表示使 vim 显示行号 nu 是 number 缩写
“提示 warning”,是因为有的电脑可以支持加速指令,
但是运行代码时并没有启动这些指令。
“提示 warning”暂时屏蔽掉。主目录下的 bashrc 文件,
加入这样一句 export TF_CPP_MIN_LOG_LEVEL=2,把“提示warning”等级降低
“0”(显示所有信息)
“1”(不显示 info),
“2”代表不显示 warning,
“3”代表不显示 error。一般不建议设置成 3
source 命令用于重新执行修改的初始化文件
使之立即生效,而不必注销并重新登录。
代码示例
随机产生 32 组生产出的零件的体积和重量,训练 3000 轮,每 500 轮输出一次损
失函数。下面我们通过源代码进一步理解神经网络的实现过程:
# -*- coding: utf-8 -*- # @File : 搭建神经网络八股.py # @Date : 2018-06-02 # 搭建神经网络的八股 # 准备工作 -> 前向传播 -> 反向传播 -> 循环迭代 # 1、导入模块,生成模拟数据集; import tensorflow as tf import numpy as np BACH_SIZE = 8 SEED = 23455 # 基于随机数产生 32行2列的随机数 rng = np.random.RandomState(SEED) X = rng.rand(32, 2) # 随机数组, 浮点数,[0, 1)均匀分布 # 输入数据集的标签(正确答案)x0+x11 x0+x1>=1 -> 0 Y = [[int(x0 + x1 < 1)] for (x0, x1) in X] print("X: \n%s"%X) print("Y: \n%s"%Y) # 2、定义神经网络的输入、参数和输出,定义前向传播过程; x = tf.placeholder(tf.float32, shape=(None, 2)) y_ = tf.placeholder(tf.float32, shape=(None, 1)) # 生成正态分布随机数,形状两行三列,标准差是 1,随机种子是 1 w1 = tf.Variable(tf.random_normal(shape=[2, 3], stddev=1, seed=1)) w2 = tf.Variable(tf.random_normal(shape=[3, 1], stddev=1, seed=1)) a = tf.matmul(x, w1) y = tf.matmul(a, w2) # 3、定义损失函数及反向传播方法 # 均方误差 loss = tf.reduce_mean(tf.square(y - y_)) # 随机梯度下降算法,使参数沿着梯度的反方向,即总损失减小的方向移动,实现更新参数。 train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss) # 4、生成会话,训练 STEPS 轮 with tf.Session() as session: init_option = tf.global_variables_initializer() session.run(init_option) # 输出未经训练的参数值 print("w1: \n", session.run(w1)) print("w2 \n", session.run(w2)) print("\n") # 训练模型 STEPS = 3000 for i in range(STEPS): start = (i*BACH_SIZE)%32 end = start + BACH_SIZE session.run(train_step, feed_dict={x: X[start: end], y_: Y[start: end]}) if i %500 == 0: total_loss = session.run(loss, feed_dict={x: X, y_:Y}) print("ssetp %d, loss %s"% (i, total_loss)) # 训练后的取值 print("w1\n", session.run(w1)) print("w2\n", session.run(w2)) """ 由神经网络的实现结果,我们可以看出,总共训练 3000 轮,每轮从 X 的数据集 和 Y 的标签中抽取相对应的从 start 开始到 end 结束个特征值和标签,喂入神经 网络,用 sess.run 求出 loss,每 500 轮打印一次 loss 值。经过 3000 轮后,我 们打印出最终训练好的参数 w1、w2。 """
